可视化并度量 BERT 的几何结构 | 少年游

type

status

date

slug

summary

1、背景介绍、相关研究和前人工作

前人的工作：

本文以 John Hewitt 和 Chistopher D. Manning的 A Structural Probe for Finding Syntax in Word Representations为基础。本文的主要贡献是：

BERT的激活空间中有整个依赖解析树的几何表示

在第 16 层（BERT-large）
应用单个全局线性变换（他们称为结构探针）后

上下文嵌入之间的距离平方与依赖解析中的树距离大致成正比

作者无法解释

这篇文章的发现：

BERT 在单独的句法和语义子空间中存储语言特征的证据

已发现 2 个表示句法和语义子空间的线性变换
这些应该是彼此正交的
注意力矩阵似乎包含相当数量的句法信息

休伊特和曼宁发现的表示几何的数学论证

毕达哥拉斯嵌入（平方嵌入）很可能是对观察到的距离的解释
可视化

BERT 具有细粒度的词义几何表示

不同的词义构建分离良好的集群
在这些集群中，上下文嵌入似乎编码了额外的细粒度含义

上面这些前人工作和本文发现的总结都来自下面可参考文章链接的机翻

Visualizing and Measuring the Geometry of BERT · Wiki · Avishek Anand / interpretability

This paper builds on A Structural Probe for Finding Syntax in Word Representations by John Hewitt and Chistopher D. Manning.

https://git.l3s.uni-hannover.de/anand/interpretability/-/wikis/Visualizing-and-Measuring-the-Geometry-of-BERT

“”

①背景介绍

语言是由离散结构构成的，而神经网络是在连续数据（即高维空间的向量）上运算的。语言处理网络需要将这些符号信息转换成某种几何形式来表示，而词嵌入（Word Embedding）提供了两个众所周知的样例:用距离来编码语义相似性，而某些方向则对应词语的极性(例如男性和女性)。

全新的表示形式：句子的句法结构是句子语言信息的一个重要组成部分。这个结构可以用树来表示，它的节点则对应于句子中的单词。休伊特(Hewitt)和曼宁(Manning)在《一种用于在单词表示中查找语法的结构探针》中指出，一些语言处理网络构造了这种语法树的几何副本。而单词是在高维空间中给定的位置，并且(经过一定的转换)这些位置之间的欧氏距离（Euclidean distance）可以映射到树的距离。但是这样同样引入了新的问题：树的距离与欧氏距离之间的映射不是线性的。相反，休伊特和曼宁发现树的距离对应着欧氏距离的平方。他们于是提出了为什么需要平方距离，以及是否存在其他可能的映射的问题。

这篇论文为上述难题提供了一些可能的答案：本篇论文的工作就是扩展了对内部表示几何的这些探索；研究BERT如何表示语法；解释休伊特(Hewitt)和曼宁(Manning)在《一种用于在单词表示中查找语法的结构探针》中描述的语法树嵌入；对于语义，展示了BERT在非常精细的层次上区分词义的暗示性证据。此外，许多语义信息似乎是在相对低维的子空间中编码。

②相关研究及前人工作

研究的对象是基于 Transformer (变换器)的双向编码器表示 (BERT) 技术： BERT的输入基于一系列标记（单词或单词片段）。输出是一个向量序列，每个输入标记对应一个向量，向量包括关于标记的上下文的信息，通常将这些向量成为上下文嵌入。

通过对大量无标号文本数据的预训练模型来探究学习语言表征始于Word2Vec与GloVe中词的嵌入，这些嵌入的局限性在于他们使用了非常浅显的语言模型。这意味着它们能够捕获的信息量有限；另一个关键性的制约因素是：这些模式没有考虑到该词的上下文。如同一个词在不同的语境中有不同的含义。然而，像Word2vec这样的嵌入将在上下文中为“bank”提供相同的向量。自然语言处理社区用ELMo处理多义词，同一个单词可以基于其上下文具有多个ELMo嵌入，ULMFiT在这一点做得更深入。

2、关于注意力矩阵的相关实验（证明Attention学习到了词之间的依赖关系（依存关系））

关于注意力矩阵的相关实验

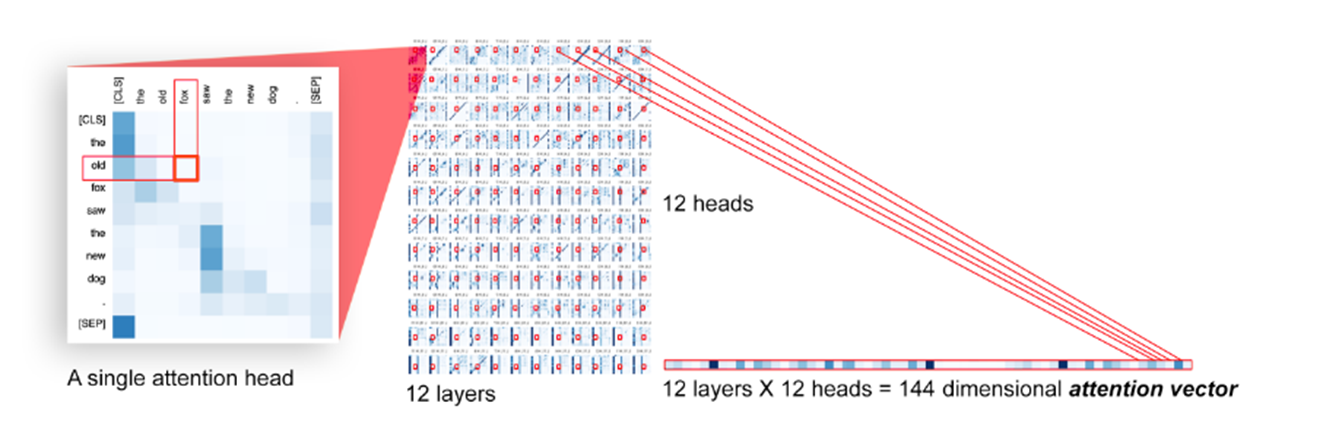
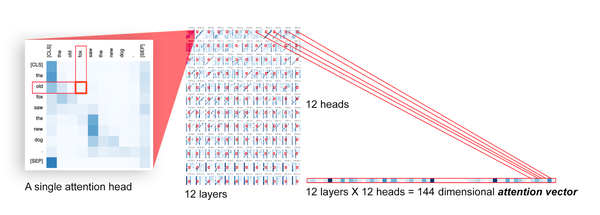
为了形式化表示注意矩阵编码语言特征的意义，我们使用了一个注意探针，注意探测是对令牌(tokeni, tokenj)的任务，其中输入是一个模型范围的注意向量，通过连接每个层中每个注意头的每个注意矩阵中的条目aij而形成。

数据集：Penn Treebank选取其中30个依赖（超过5000个样本）

利用这些标记嵌入，我们通过随机梯度下降训练两个L2正则化线性分类器，一个二分类用于判断是否存在依赖一个多分类，判断是哪种依赖如果正确性大于阈值说明Attention编码了依赖关系二元探针的准确率为85.8%，多级探针的准确率为71.9%。这种简单的线性探测的成功表明，句法信息实际上是编码在注意向量中。

“”

3、树嵌入的数学解释和可视化

“”

句子的句法结构是句子语言信息的一个重要组成部分。这个结构可以用树来表示，它的节点则对应于句子中的单词。休伊特(Hewitt)和曼宁(Manning)在《A structural probe for finding syntax in word representations》中指出，一些语言处理网络构造了这种语法树的几何副本。而单词是在高维空间中给定的位置，并且(经过一定的转换)这些位置之间的欧氏距离（Euclidean distance）可以映射到树的距离。树的距离与欧氏距离之间的映射不是线性的。相反，Hewitt和Manning发现树的距离对应着欧氏距离的平方。

欧几里得空间的树嵌入：

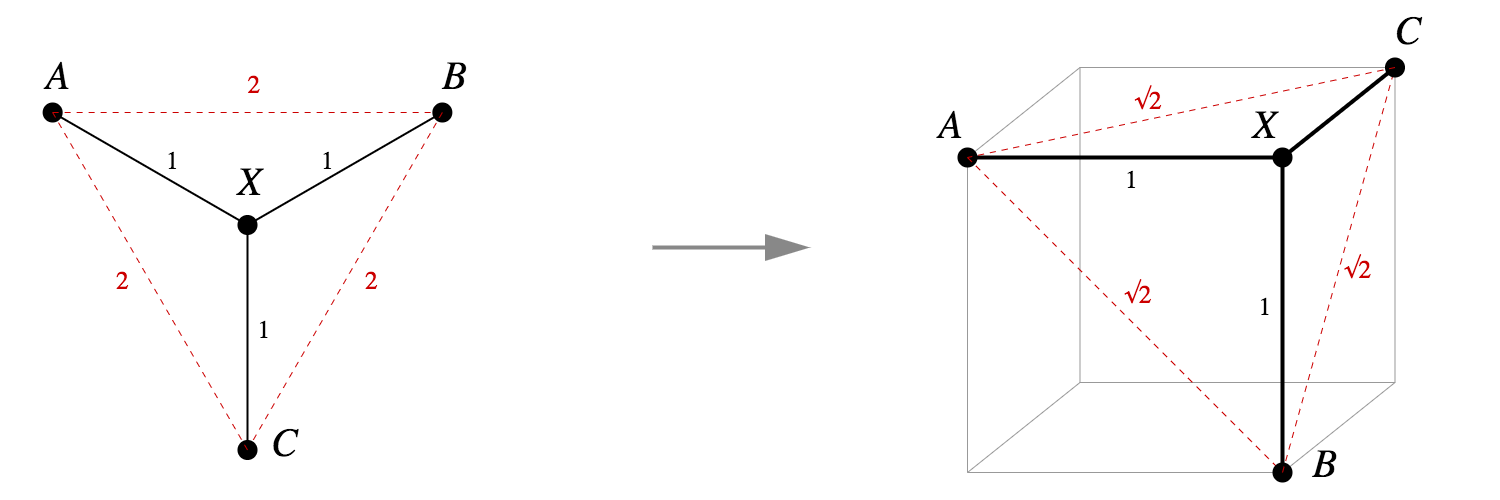
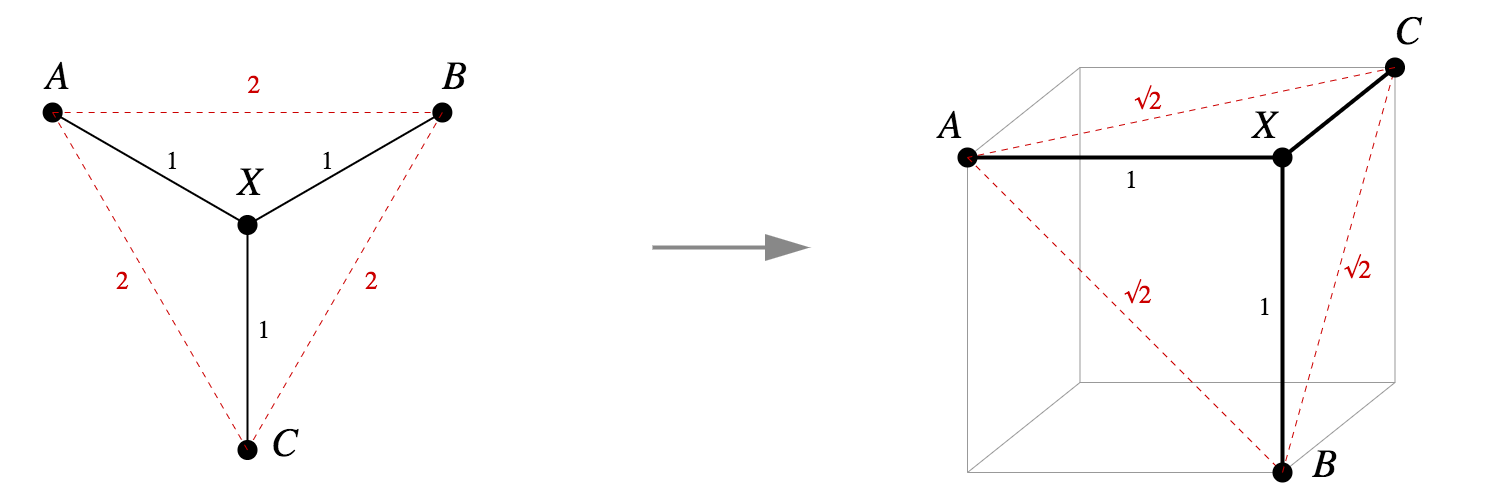
如果这个树有分支，则无法实现等距离扩展。

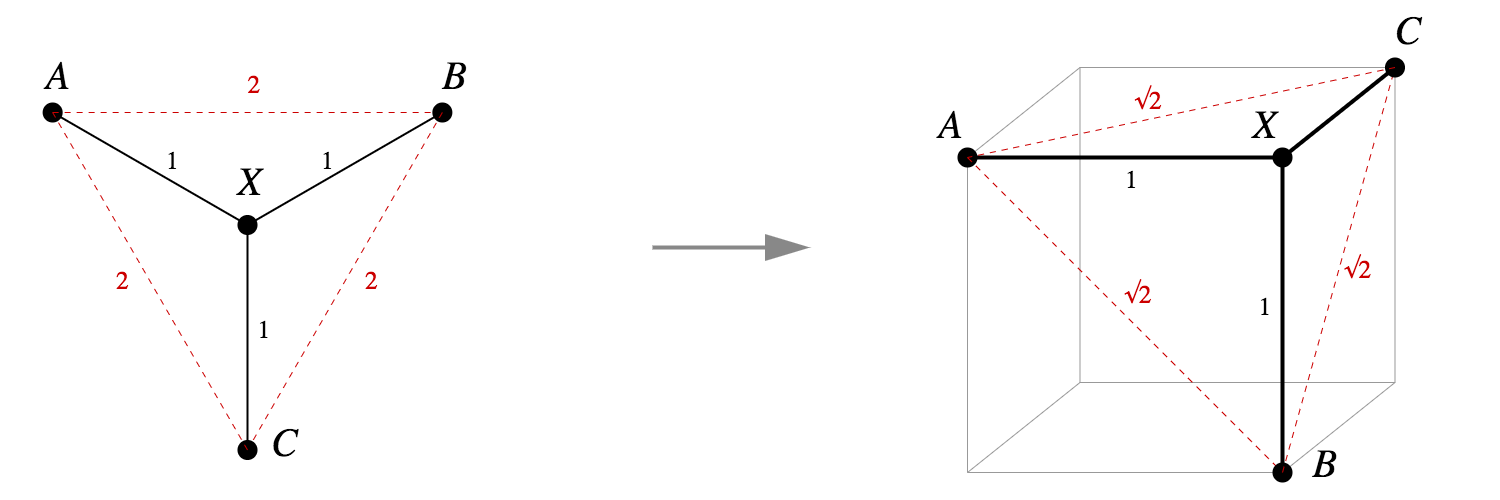
事实上，图 1 中的树就是一个标准示例，表明并非所有度量空间都可以等距离地嵌入到中。因为，所以在任意嵌入中 A、X 和 B 都是共线的。基于同一逻辑，A、X 和 C 也是共线的。但这就意味着 B=C，这是矛盾的。

毕达哥拉斯嵌入（Pythagorean embeddings）：

相反，平方距离嵌入实际上要好得多——它是如此好用以至于有专属名称，令 M 为一个度量空间，其度量为 d。如果对于所有，我们有：为一个毕达哥拉斯嵌入。

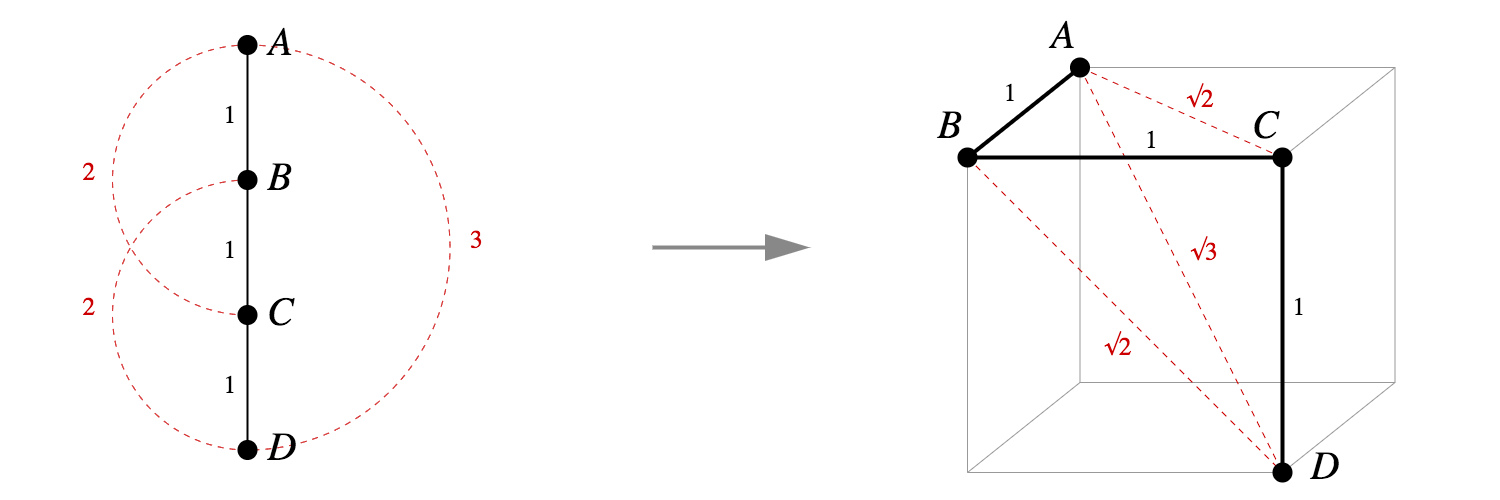
对于理论上的树嵌入，d(A,B)=d(B,C)=d(C,D)=1，d(A,C)=d(B,D)=2，d(A,D)=3，那么ABCD一定是共线的；使用毕达哥拉斯嵌入则可以在正方体的顶点中有很好的嵌入。

定义1：令 M 为一个度量空间，其度量为 d。设如果对于所有的 x,y∈M，都有：

则我们说 f:M→R^n 是幂为 p 的嵌入

定理1：任何有 n 个节点的树都有在 R^(n-1) 中的毕达哥拉斯嵌入：

令树 T 的节点为，其中 t_0 为根节点。令为的正交单位基向量。经过归纳，定义一个嵌入：

给定两个不同的树节点 x 和 y，m 是它们的树距离 d(x,y)，则我们可使用 m 个互相垂直的单位步从 f(x) 移动到 f(y)，因此：

这种证明的价值不仅在于结果本身，而且在于其能够显式地几何构造出一个结果。任何同一树结构的两个毕达哥拉斯嵌入都是等构的，并且通过旋转或反射相互关联，每对点之间的距离在这两种情况下都是相同的。我们可以说这是树结构的毕达哥拉斯嵌入，这个定理清楚地告诉我们它的结构是什么样的。

此外，定理1中的嵌入有一个清晰的非正式描述：在图中的每个嵌入顶点上，所有到相邻顶点的线段都是彼此正交的单位距离线段，并且与每条边都正交。查看PPT第一张图片，可以看到它们符合是这个描述的。

我们也很容易看到在证明中构造的特定嵌入是一个ℓ1度量中等构的树，尽管这很大程度上依赖于轴对齐。

我们可以对定理1.1做一个简单的推广。考虑有边权值的树，与两个节点之间的距离是它们之间最短路径的边权值之和。在这种情况下，我们也总是可以创建一个毕达哥拉斯嵌入。

虽然使用的名字各不相同，但一般度量空间的幂为 p 的嵌入已被研究了数十年。这方面的奠基工作是 Schoenberg 1937 年的论文：《On Certain Metric Spaces Arising From Euclidean Spaces by a Change of Metric and Their Imbedding in Hilbert Space》。

该论文的一个关键结果用术语说来就是：

如果一个度量空间 M 有在 R^n 中的幂为 p 的嵌入，那么对于任意 q>p，它也有幂为 q 的嵌入。因此当 p>2 时，任意树都总是有幂为 p 的嵌入。
而 p=2 的情况则很不一样，还没有一种用于描述这种嵌入的几何性质的简单方法。
对于任何给定的p<2，都没有足够的 “room” 来嵌入一个有非常多子节点的节点。

毕达哥拉斯定理树嵌入的简单性，以及它可以被一个简单的随机模型近似的事实，表明它可能是需要双曲几何（require hyperbolic geometry）的树嵌入方法的一个相当实用的替代品。

树嵌入的可视化

BERT中的解析树嵌入与精确的power-2嵌入相比如何？为了研究这些差异，论文作者创建了一种简单的可视化工具。该工具的输入是带有相关的依存解析树的来自Penn Treebank的句子。然后提取了BERT-large在第16层产生的标记嵌入，经过 Hewitt 和 Manning 的「结构探针」矩阵的变换，得到一个在 1024 维空间中的点集。然后，我们通过 PCA （主成分分析）将这些点映射到二维（其他降维方法如t-SNE和UMAP，将更难解释）。

为了展现其底层的树结构（使树结构可视化），连接表示有依存关系的词的点对，每条边的颜色表示与真实树的距离的偏差。用虚线连接没有依存关系的词的点对，但它们的位置（在经过PCA处理之前）远比预期的要近。由此产生的图像让我们看到了树嵌入的整体形状，以及与真正的幂-2嵌入（power-2 embedding）的偏离的细粒度信息。

下图展示了样本句子的结果。

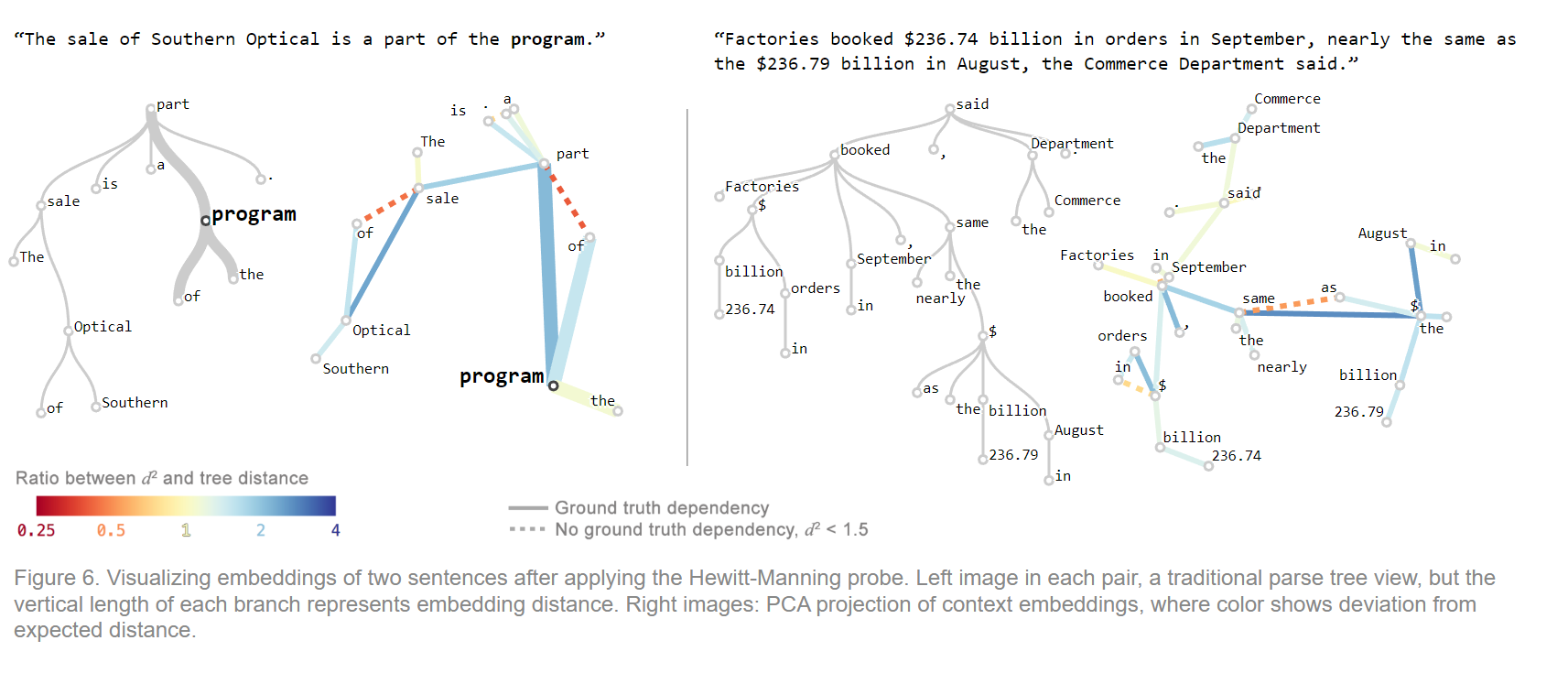
可交互版本：

Language, trees, and geometry in neural networks

https://pair-code.github.io/interpretability/bert-tree/

Language, trees, and geometry in neural networks

左图使用的是传统的解析树视图，每个分支的垂直长度代表嵌入距离；右图为经过PCA处理的上下文嵌入，其中颜色表示与预期距离的偏差。

具有特定依存关系的两个词之间的平均平方边长。

这些是典型的案例，说明了一些常见的模式；例如：介词在预料之外地被嵌入到它们相关的词的附近。

一个自然产生的问题是，这些投射（projected）树和典型（canonical）树之间的差异是否只是噪音，或者是更有趣的模式。通过观察每个依存关系的平均嵌入距离，我们可以看到它们的差异很大，从大约1.2（compound:prt，advcl）到2.5（mwe，parataxis，auxpass）。这种系统性的差异表明，BERT的句法表示（syntactic representation）在传统的依存关系句法之外还有一个额外的量化方面（quantitative aspect）。

“”

4、语义的几何结构（BERT是否能区分不同上下文情况下的语境）

在这部分，文章从BERT模型内所使用transformer结构出发，作者指出，transformer模型的嵌入结果是基于上下文的，呢么我们也可以推测，BERT同样能获取到一个词汇在具体语境中的含义。例如BERT应当能区分“bark”这个单词在某一个句子中到底指的是动物的叫声还是树皮。本篇论文从定性和定量的角度研究了词义的几何结构表示。

4.1 词义的几何结构的定性表示（可视化分析）

作者收集了英文版维基百科上所有文章的简介部分的数据，而后做了一个可交互的应用，其使用过程为：

用户输入一个单词

系统会找到至多1000条包含该词的句子，并用这些句子作为BERT-base的输入

用户可以检索该BERT模型对于这些输入在不同的层下的上下文嵌入结果

系统使用UMAP进行结果的可视化呈现

下图展示了使用UMAP工具对不同语境下 “die”的嵌入向量进行可视化的结果：

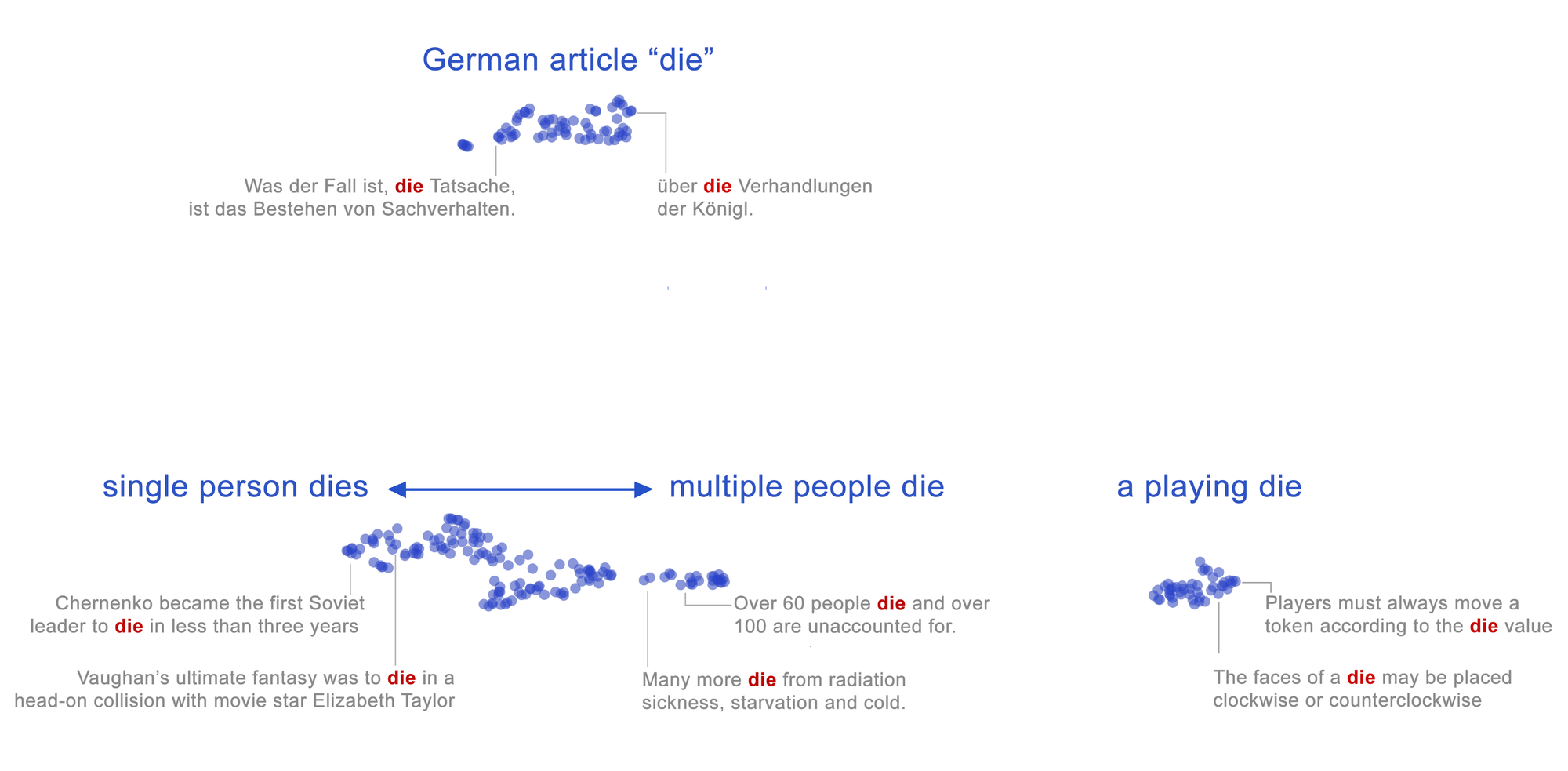
文章指出，从图中我们可以发现一下特点：

不同的词义在空间上是分开的，如死亡、冠词、骰子三种含义在可视化后的结果上有不同位置的空间分布。

同一集群内包含着细粒度的词义差别，图中不同上下文的死亡（死亡人数差异）通过空间上位置的偏移体现出来，单个人的死亡在图中的分布偏左，群体的死亡偏右。

上述两点总结了词义的几何结构的定性特征，由此，文章作者进一步特出问题：

1、能否定量地衡量其包含的词义信息？ 2、前文已说明词嵌入表征了句法信息，这里又说明表征了词义信息，是否冲突？

下面的工作用以解决这些疑问：

4.2 词义消歧能力的定量分析

作者按照Peters 等人描述的程序（他们使用 ELMo 模型进行实验），同样训练了一个简单的最近邻分类器来执行词义消歧 (WSD)任务。

该实验的数据集参考了Raganato 等人的文章，使用来自 SemCor的数据，这是一个人工语义标注语料库。经过筛选，本实验中训练集使用33,362 条词义，测试集使用3,669 条词义。

实验的分类方法比较简单：对于具有 n 个含义的给定单词，在该最近邻分类器中，设置n个点，每个点都是训练数据中同一含义的BERT-base嵌入结果集群的质心点。最接近的输入的新词嵌入结果对应点的那个一个作为分类结果输出，如果训练数据中不存在该词，则默认选择最常用的词义。

实验结果以表格的形式呈现如下：

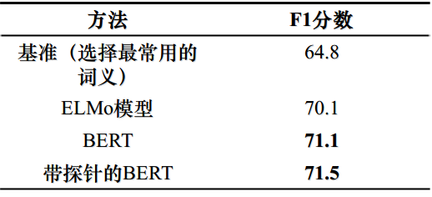
可以看到，BERT在简单的最近邻分类器下获得了 71.1 的 F1 分数，高于ELMo模型，准确度在各层中单调递增，说明上下文嵌入结果能够表征词义信息。并且从定量的结果来看，其效果比当时最好的模型ELMo还要好一些。

此外，带探针的BERT获得了 71.5 的更高分数，该技术在后面将会提到。

4.3 词义包含在嵌入子空间内

前文中提到Hewitt 和 Manning通过一个称作结构探针的矩阵对上下文嵌入进行变换发现其包含句法信息的嵌入子空间。类似的，本文作者假设可能还存在一个语义子空间。也就是说，在适当的线性变换下，相同意义的词会靠得更近，不同意义的词会更远。为了探索这个假设，作者按照Hewitt 和 Manning的方法训练了一个探针。

其基本的训练方法如下：

初始化一个随机矩阵𝐵∈^(𝑘×𝑚)，在不同的维度m下测试，损失(loss) 定义为相同与不同含义的词嵌入各自平均余弦相似度的差，loss被限制收敛在±0.1内。在训练数据集上，使用的是前文SemCor 数据集中具有至少两种含义的单词，每种含义至少出现两次（共筛出原始 33,362 种词义中的 8,542 种），通过BERT-base（12层，768维）获得嵌入数据。

从我对该实验的理解来看，BERT得到的词嵌入结果就是一个矩阵（向量），作者希望借助一个探针（也是一个矩阵），把这两个矩阵相乘（也就是文章中提到的所谓适当的线性变换），相乘得到的新矩阵希望能把一个词的不同词义区分地更好一些，直观地就是在可视化结果上不同的集群（聚簇）能相隔更远一些。同时作者又对损失函数进行了限制，从原文上看，这么做的限制似乎是防止一味地放大词义上的差异而损失了别的信息，所以文章不让不同词义的余弦相似度差值太大（不要分得太开了）。

作者把经过探针变换后的新矩阵用于前面的词义消歧定量实验中：

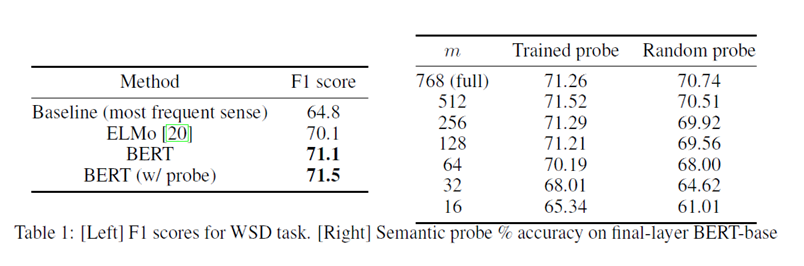
上图右侧表格描述了实验结果，作为对照，将每个经过训练的探针与相同形状的随机探针进行比较。结果表明：训练好的探针能够将F1得分略微提高，直到到 m = 128 维左右的瓶颈。

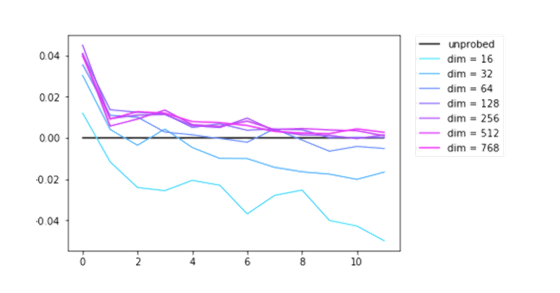
文章在附录部分披露了实验更多的信息，上图应当是不同维度下探针运用后各层分类准确率的变化（文章作者没有给出更加明确的图例）。作者指出，尽管在最后一层只稍微提升了准确率，但探针可以更大幅度地改善早期层的性能。这表明较早的层内上下文嵌入的几何结构中存在更多的语义信息。

以此同时，实验结果支持了词义信息可能包含在低维空间中的观点。即能说明：词嵌入同时编码了句法和词义，但可能在不同的的互补子空间中。对于这一结论，文章附录部分给出了部分补充：

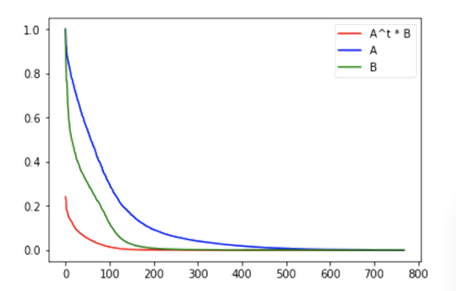
作者将的词义消歧探针 (A) 与 Hewitt 和 Manning 的句法探针 (B) 进行了比较。发现 AT ∗ B 的奇异值比单独的 A 或 B 的奇异值更快地降为零：对于 A ∗ BT 的奇异值也是如此。这表明 A 和 B 彼此正交。

文章仅对该观点进行了这么多解释，图表中的一些细节并更具体的说明，因此在这个观点上我自己阅读时也仍存在一些疑惑。

4.4 嵌入距离和上下文语境的联动实验

这个实验用于进一步验证BERT是否真的编码了上下文语境信息（即区分词汇在不同语境中的不同含义）。BERT中词义受上下文影响，并由空间位置编码。文章认为应该能够通过系统地改变上下文来影响BERT上下文嵌入结果的位置。为了检验这个假设，作者行了一项简单且可控的上下文变化的实验，实验的核心就是“将各自使用同一个词的不同含义的两个句子连接起来”。

假设一个词有两个词义A和B，并且所有词义嵌入取平均值对应位置为A-center和B-center，那么从使用词义A中的句子内计算词嵌入，其到A-center的距离DA应该比到B-center的DB更近，余弦距离越接近1，即有距离比率DA / DB > 1。

本实验再把A对应的句子和B对应的句子用and连接成一句话，放进BERT中计算得到嵌入结果，与原来距离比率作比较。理论上其词嵌入结果到两个中心的距离应该发生了偏移，而且应该和原先的单纯A含义的句子相比，结果应该更靠近比中心一些。实验结果也证明了这一推测：

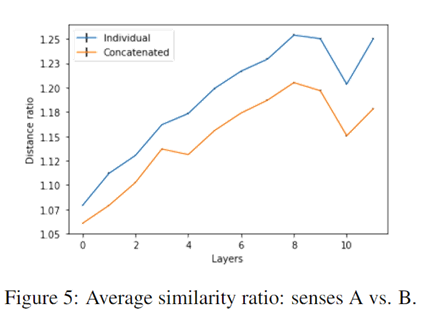
作者仍然没有给出图表具体的说明，结合文章有限的说明，上图数据应当是某个词汇嵌入数据在不同层的距离比率，蓝色对应单句，黄色对应and连接后的句子。

作者通过实验给出以下结论：

串联句子中的其他含义的嵌入使得结果移向另一个含义的中心，对应的距离比率变小了

连接一个随机句子并没有改变个体的相似比

与单个句子相比，连接句子中最后一层嵌入的错误分类率明显更高：分别为 8.23% 和 2.43%。

在将每个嵌入与我们之前训练的语义探针相乘后，缓解了距离比率的减小，降低了分类错误率：串联句子为 7.31%，单个句子为 2.27%

实验结果说明，同一词汇在不同上下文条件下的BERT嵌入结果是有系统性差异的。（特别的，这里的不同上下文条件的创造是无逻辑性的，也就是实验不管and连接的两个句子有没有关联，生硬地连接在一起）文章指出，这个无逻辑性的条件也说明了基于注意力的模型的潜在隐患：在关注上下文信息时不会遵守语义边界，常常是不加选择地从所有上下文中记录信息。这个语义边界的概念我并没有找到很详细的说明，我个人对此的理解就是说BERT在编码上下文信息的时候并不关注句子整体的逻辑性，由此可能带来问题或缺失一些信息。

本人制作的ppt部分如下：